先日、指導している際に気になることがありました。昔から何度も目にしていることではありましたが、これはマズいと講師が感じている理由が何なのかを今回はお伝えしようと思います。
場合の数において
指導している子が『場合の数』の単元においてこういうことを行いました。
6個のリンゴをABCの3人で残さず分けます。分け方は何通りあるでしょうか?
という問いに対して、その子は下記のように解いていました。
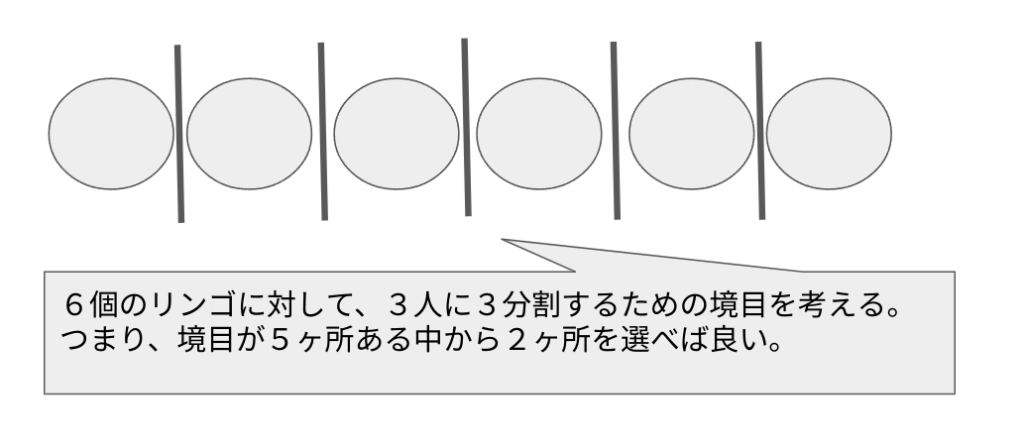
私は子供にどうしてこう解こうと思ったのかを確認しました。すると、某動画解説コンテンツでこのように解いていたから、という返事でした。正直、またかと頭を抱える思いに駆られます。この問いをこのように解く事自体は間違いではありませんが、はっきり言うと意味はありません。それどころか、生半可なレベルで行っていると後々全然分かっていないという状態になるケースも散見されます。
本来は必ずこの問いは下記のような解き方で解くことを練習すべきです。
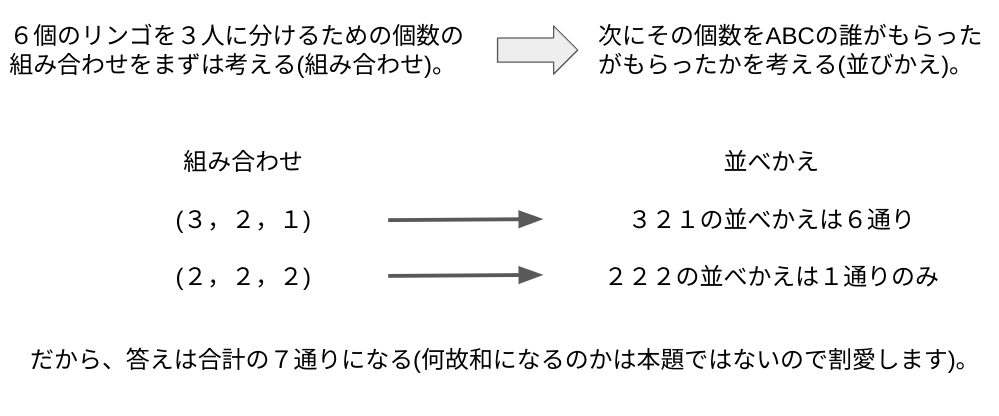
※訂正
組み合わせに(4,1,1)もあります。この並べかえは3通りになるので合計は10通りです。
この考え方を中学受験では『和分解』と言います。この考え方は組み合わせ→並べかえというように2段階に分けて問いを考えることが要点になります。では、何故上記の境目の解き方を行うことが良くないのかの理由は下記のことが考えられます。
①必要な練習になっていない
子供は大人が想像する以上に『規則正しく行う』ということを苦手としています。
その内容がかなり影響する単元の一つが『場合の数』と言えます。その一つとして上記の『組み合わせ』を漏れなくミスなく書き出すということが非常に出来にくいです。
規則正しく行うことを私は『順序よく書き出す』と説明しておりますが、これに関して子供がミスして行うことは
- 思いつくまま書いていく
- 順番を守らず、もしくは最初から考えてもいなく適当に書いていく
が代表的でしょう。子供は自然にしたら無秩序です、そのままであれば上記のようなことを行うことは当然と言えます。それを、秩序を理解しルールを守り漏れなくミスなく調べ上げれるように練習しなければならないわけです。その重要な観点から考えれば、境目の解き方で解けたとしても今後の中学受験の内容に繋がらないわけです。
実際に組み合わせを書き出す際に必要な考えは、重複を避けるために順番を戻らないことや、数字を一つずつ変えていくことです。きちんと積み上げている子は自然に身に着けていく技術ですが、まともな積み上げが無い子はいつになっても身についていない内容です。
使える時・使えない時の見極めが必要
上記の境い目の考え方は例に挙げた問いでは使えます。しかし、少し内容を変えるともう使えなくなります。例えばこういう問いです。
こうなると境い目の考え方は使えません、少し内容を変えただけなのに何故でしょうか?
それは0を使うからです。
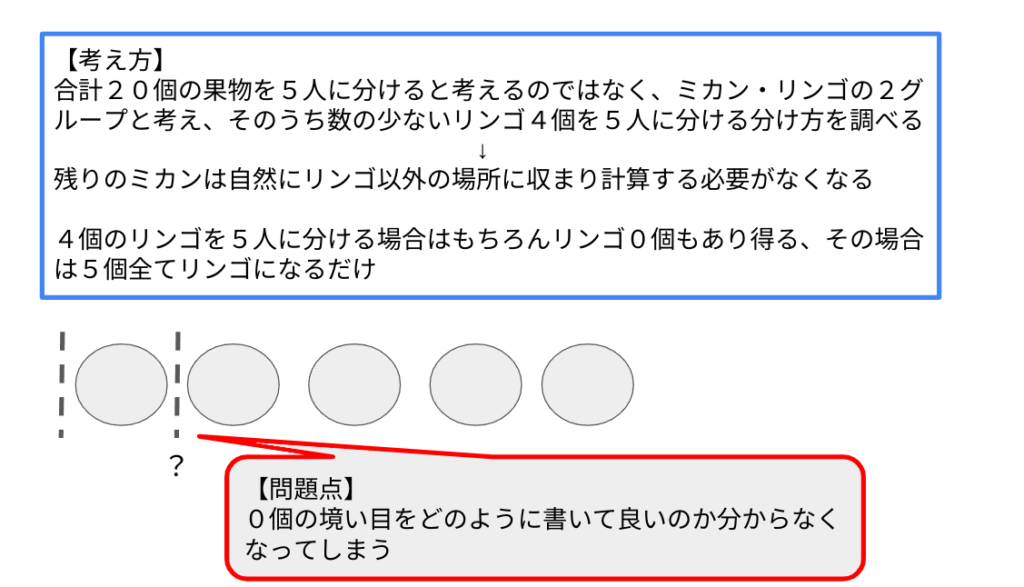
上記のように0個の境い目を考える時どうやって書いて良いのか分からなくなります。このようにほんの一部を変えられてしまうと対応が利かなくなるやり方を覚えることに意味があるのでしょうか?
もちろん、和分解の考え方で組み合わせを見つけることは今回も対応できています。
ちなみに、やり方を考えると上記の問いも境い目の考え方で対応させることは可能です。興味のある方は考えてみて下さい。
しかし、この程度の変化でわざわざ工夫をしなければならないことを覚えることに意味は無いと私は思っています。
一番ダメなことは解き方のコレクション
私が一番ダメだと思うことは、『解き方のコレクション』を行うことです。
上記の場合の数の例で言えば、和分解で組み合わせを漏れなく書き出す訓練を積むことをせず、計算だけで出せる境い目の考え方で解いてしまうことがそれに該当します。
では何故『解き方のコレクション』を行うことがダメなのでしょう。理由は2つあります。
①コレクションには限界がある
まず一つ目の理由は、単純に限界がすぐ来るからです。実際に何かをコレクションした際にも、無限に集め続けることは物理的に無理です。仮にコレクション用にいくらでもスペースを用意できる程の資産家でなければすぐに物で溢れかえってしまいます。
それと同じことで、解き方も一つずつは大したことがないように思えてもそれを全単元において一々問題ごとの解き方を覚えようとすると膨大になってしまいます。しかも、受験勉強の場合は他に知識科目があります。そこではどうしても多くの知識を覚えていかなければなりません、そこに算数まで同じことをしたならば異様に記憶力に優れた子供しか出来ないということになってしまいます。
②無駄が多い勉強になる
はっきり言ってしまえば、細かい知識というのはあくまでオマケです。中心となるのはその単元で最も汎用性が高い考え方・解き方を理解し定着させることです。結局はそれがまずはメインとなり、同じ内容の様々な問いに対応が利くようになっていきます。細かい知識的な解き方はあくまで枝葉に過ぎません。メインとして大きな幹が出来ていなければ、枝葉を増やすと幹自体が崩れて倒れるケースまであります。このケースはかなり厄介で、5年生ぐらいまでは好成績を修めていても途中から急落する場合の子に当てはまることが多く、立て直しに非常に手こずります。理由はメインとしての大きな幹が無いか弱々しく、まずはそこを立て直さなければならないからです。この幹・枝葉のイメージは下記のようなものでしょうか。
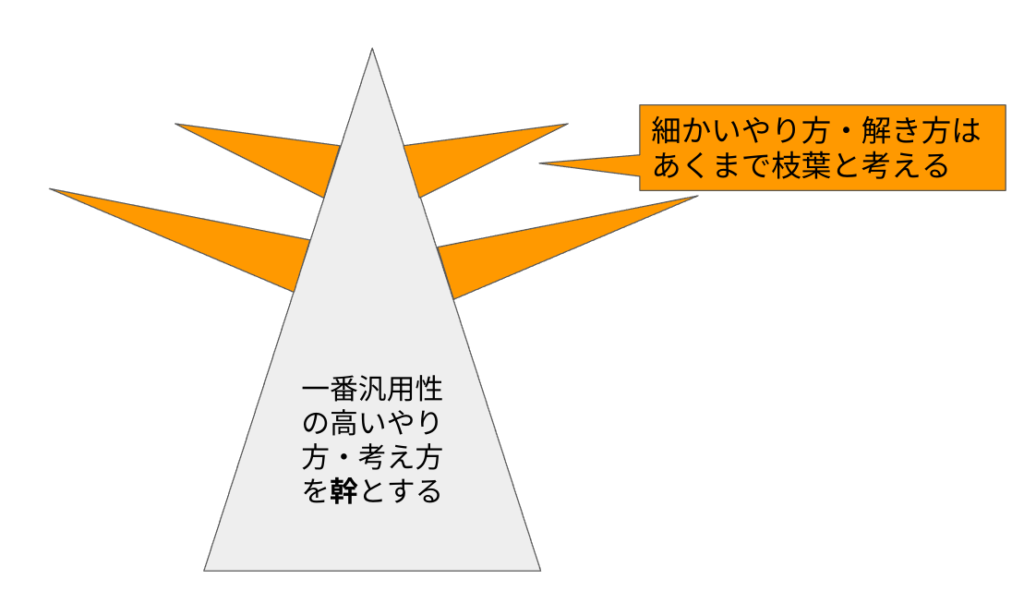
そのため、一度学習した内容ももう一度やり直さなければならなく、非常に無駄です。しかも本人に相当な覚悟がなければ、もう一度やり直すことに抵抗感があることも忘れてはいけません。
③本質的な内容の理解から逃げる
最後に一番影響の出る理由が、上記のようなテクニック的な解き方を覚えようとする子は本質的な内容から逃げこうやったら解けるという解放を丸暗記するケースがとても多いということです。
これが何故マズいのかは、問いを解くという観点での問題は②の理由からです。もう一つ、子供自身の姿勢・意識の観点での問題点が考えられ、それは『考える』ことを放棄しているということです。実は基本的な論理をしっかりと根底から理解し定着することはとても頭を使って考えることを要求されます、状況を考えや内容をときには具体的な内容に置き換えて想像したり、さらに逆に理解した文章の内容を一般化することも大きく求められます。その上で何度も練習し、理解した内容を一々考えなくても条件反射で答えられるようにしなければなりません。これは子供にとって非常に大変な作業になります。だから、そこから逃げ、安易にこうすれば解けるという内容に飛びついてしまう子はいるのです。
こういった、裏技的な内容は子供にはキャッチャーに受け取られ目先はひくことが出来ると思います。だからこそ、実力のない講師はこういうことばかり教えがちです。
まとめ
昔から『○○の裏技集』などの上記のようなテクニック集的なものはありました。しかし、例外なくこういったものに頼ろうとする子の算数は大して伸びません。理由としては
①コレクションになっている
②無駄が多い
③考えることから逃げてしまっている
というようなことでしょう。残念ながら本質的な内容から逃げて上手くいくことはありません。
それでは、どうすればこういった失敗を回避し本質的な学習を子供が行えるようになるのかというと、いくつかのステップが考えられます。
・子供が算数の内容を理解していると思えない
↓
・まずは塾に相談する
↓
・相談して聞けた改善方法を子供任せにせず、保護者がチェックしつつ行う(最低一ヶ月ほどは続けましょう)
↓
・それでも改善が見られない
上記を行い、それでも改善が見られない場合は
ゴール(入試)から内容を逆算できその時ごとに必要な内容を理解している人物がサポートする
という方法しかないと思われます。
塾や市販教材の中には、子供向けに説明が載っているものもありますが、この状況に陥っている場合はそれでは難しいでしょう。残念ながら、教材での説明を理解するには自力で考えなければなりません。自分で考えることをしないことが問題点なのに、解決方法が自分で考えることならば矛盾しております。
サポートをする人物もよくよく選定をして下さい。経歴・方法論・行動など様々なものを考え検討なさって下さい。
残念ながら、現在の中学受験を取り巻く環境を考えると塾のみで成功することは難しい子供が増えております。保護者の方が先を考え、子供にとって本当の意味で意味のある時間を積み重ねられるかどうかが成否に直結致します。是非、子供の将来に繋がる受験にしていきましょう。



